Il minimo comune multiplo (MCM) è un concetto fondamentale nell’aritmetica e nella matematica in generale. Serve come base per risolvere problemi che coinvolgono frazioni, divisori, e multipli. In questo articolo, esploreremo nel dettaglio cosa sia l’MCM, le sue regole, come calcolarlo, e vedremo esempi pratici per comprendere meglio questo importante strumento matematico.
Cosa è il Minimo Comune Multiplo?
Il minimo comune multiplo è definito come il più piccolo multiplo comune tra due o più numeri. In altre parole, l’MCM di un insieme di numeri è il più piccolo numero che è divisibile per ciascuno di questi numeri.
Ad esempio, consideriamo i numeri 4 e 6. I multipli di 4 sono:
4, 8, 12, 16, 20,…
e i multipli di 6 sono:
6, 12, 18, 24,…
Il multiplo comune più piccolo tra i due è 12. Quindi, il minimo comune multiplo di 4 e 6 è 12.
A cosa serve il Minimo Comune Multiplo?
L’MCM è utile in molti contesti matematici e pratici, tra cui:
- Somma e sottrazione di frazioni
Per sommare o sottrarre frazioni con denominatori diversi, è necessario portarle ad un denominatore comune. Questo denominatore comune è spesso l’MCM dei denominatori delle frazioni. - Sincronizzazione di eventi periodici
Se due o più eventi si ripetono a intervalli regolari, l’MCM dei loro periodi fornisce il tempo minimo in cui tutti gli eventi si verificheranno simultaneamente. - Problemi di divisibilità e multipli
L’MCM viene utilizzato anche per risolvere problemi che coinvolgono multipli comuni in ambiti come la teoria dei numeri.
Regole per il calcolo del Minimo Comune Multiplo
Ci sono diversi metodi per calcolare l’MCM. Vediamo le tecniche più comuni:
1. Metodo della lista dei multipli
Questo metodo consiste nel scrivere i multipli di ciascun numero e trovare il più piccolo multiplo comune. Sebbene sia intuitivo, può diventare poco pratico per numeri grandi.
Esempio: Trovare l’MCM di 3 e 5.
- Multipli di 3: 3, 6, 9, 12, 15, 18, …
- Multipli di 5: 5, 10, 15, 20, …
Il minimo multiplo comune è 15.
2. Metodo della scomposizione in fattori primi
Questo metodo sfrutta la scomposizione di ciascun numero nei suoi fattori primi. L’MCM è ottenuto prendendo il prodotto di tutti i fattori primi, ciascuno con l’esponente massimo tra quelli presenti.
Esempio: Trovare l’MCM di 12 e 18.

- Scomposizione di 12: 22 ⋅ 31
- Scomposizione di 18: 21 ⋅ 32
Moltiplichiamo insieme tutti i fattori primi presi una sola volta, con l’esponente maggiore.
L’MCM sarà 22 ⋅ 32 = 36.
3. Metodo del massimo comune divisore (MCD)
L’MCM può essere calcolato utilizzando la relazione tra MCM e MCD:
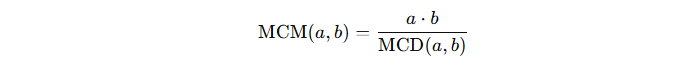
Questo metodo è particolarmente utile se si conosce già il massimo comune divisore dei numeri.
Esempio: Trovare l’MCM di 8 e 12.

Esempi Pratici
Esempio 1: MCM di 15 e 20
- Scomposizione in fattori primi:
- 15 = 3 ⋅ 5
- 20 = 22 ⋅ 5
- Prendiamo tutti i fattori con l’esponente massimo:
- 22 ⋅ 31 ⋅ 51 = 60
Quindi, l’MCM è 60.
- 22 ⋅ 31 ⋅ 51 = 60
Esempio 2: MCM di 9, 12 e 18
- Scomposizione in fattori primi:
- 9 = 32
- 12 = 22 ⋅ 31
- 18 = 21 ⋅ 32
- Prendiamo tutti i fattori con l’esponente massimo:
- 22 ⋅ 32 = 36
Quindi, l’MCM è 36.
- 22 ⋅ 32 = 36
Esercizi per praticare
- Calcola l’MCM di 14 e 21.
- Calcola l’MCM di 8, 9 e 12.
- Trova l’MCM di 24 e 36 usando la formula con l’MCD.
Curiosità e applicazioni avanzate
- Matematica modulare: L’MCM gioca un ruolo fondamentale nella teoria dei numeri e nelle equazioni modulari.
- Informatica: Gli algoritmi per calcolare l’MCM sono spesso utilizzati nei computer per risolvere problemi di sincronizzazione e gestione delle risorse.
- Frazioni equivalenti: Quando si trasformano frazioni in forma equivalente, l’MCM dei denominatori è il nuovo denominatore comune.
Conclusione
Il minimo comune multiplo è uno strumento potente e versatile che va oltre i semplici calcoli numerici. Dalla somma di frazioni ai problemi complessi di divisibilità, l’MCM è fondamentale in molti campi della matematica e della scienza. Con i metodi e gli esempi forniti, sarai in grado di calcolarlo facilmente e applicarlo nei contesti più diversi.
Potresti essere interessato
- Bilanciare la carriera e la vita privata: Consigli per il successo
- I segreti della gestione di un team di successo: Consigli dei leader
- I segreti della gestione del zempo per una massima produttività
- Come avviare una piccola impresa di successo da zero
- Idee innovative per migliorare le strategie di marketing